You’re in the fortunate position of having funds to invest. How can you choose between the numerous potential investments available to you, with their different yields, risks and durations? This question sometimes trips up even highly astute observers. Here, we’ll review some basic ways to compare returns and then look at how the return numbers of the Yearn vaults ended up having a long-standing mistake.

APR and APY

Let’s start with the basics. Boomer Bank offers an instant access bank account with 2% interest, paid once per year in arrears. Scambank also offers a similar accout, but it pays 0.5% interest per quarter. Which of these accounts is better?

If you invested $10,000 in Boomer, after a year you’d receive $200 for a total capital of $10,200. At Scambank, after the first quarter you’d receive $50, which you could add into the account. After the second quarter, you’d receive $50.25 in interest. Repeating this exercise each quarter, you’d end up with $10,201.50 in total capital at the end of the year. Both accouts have a nominal interest rate, also known as annual percentage rate (APR), of 2%. However, they have a different effective rate, of 2% and 2.015% respectively.

In the US, banks are required to disclose each account’s effective rate, also called annual percentage yield (APY). Similar legislation exists in the UK, where the effective rate is instead known as the annual equivalent rate (AER).

ROI

A zero coupon bond is a bond that does not pay interest. These days, there really are bonds which produce no economic benefit to their holder whatsoever, but over almost the entire history of financial markets, investors did require compensation for tying up their capital. Hence, zero coupon bonds would need to be issued at a discount: for example, you could buy a bond for $950 which would be redeemed for $1,000 in two years’ time, for $50 in profit, also known as imputed interest.

Since this bond does not have any interest payments, using APR and APY here isn’t quite appropriate. Instead, we can use return on investment (ROI), which is simply the gain divided by the initial capital. In our example, the $50 you’d gain translates to a ROI of 5.26% over two years.

How does the return of this bond compare to the returns of the bank account in our earlier example? We cannot compare the numbers directly, because the bond locks up funds for a longer time. We can instead annualize the bond’s return by calculating how much it grows in one year. This produces an annual ROI of 2.598%, showing that the bond indeed pays better than the two bank accounts.

A Hazy Crystal Ball

Prediction is very difficult, especially about the future.

— Niels Bohr

You may have observed that the examples make the implicit assumption that the rates do not change. If you expect that higher rates will become available in the future, you’d naturally prefer short-term investments now, so that you’d have dry powder available to make use of the better rates when they appear. Contrariwise, if you expect rates to fall, you’d prefer to lock up funds on the current good rates for as long as possible.

Generally, it is fair to assume unchanging rates for a simple reason: if we have no ability to predict future rates, then we’re equally likely to overestimate them as we are to underestimate them. Thus, the expected value of the error introduced by this assumption is zero.

Another common objection to the use of annualized returns in DeFi is that yields are so highly variable that it is futile to predict them even over the next week, let alone a full year. However, the main reason investors need such estimates is not to reliably predict outcomes over a year, but rather to compare potential investments with different time spans. For this purpose, it makes little difference whether returns are extrapolated over the period of a year, a minute or a century, as long as they are normalized to the same duration.

IRR

Let’s consider a more complex example. Remember Boomer Bank’s account from our first example. What if you invest $10,000 at the beginning of the year, then withdraw half of it after one quarter, put it back after another quarter, and finally withdraw the lot at the end of the third quarter? You would receive a total of $125 in interest, for a ROI of 1.25% based on your initial investment. The APR and APY are still 2%; it is after all the same account.

In a sense, it is unfair to calculate return on the initial investment when those funds were not fully employed through the entire period. The internal rate of return (IRR) is used to calculate total return over time in such a situation, represented as an annual rate. In our example, the IRR equals the APY at 2%, which makes sense since the interest rate didn’t change at any point.

When people in DeFi look for APYs, what they actually want to find out is the ex-ante IRR, i.e. an estimate of the IRR they will get over their investment period.

A Linear Fallacy

Finally, we’re ready to examine the return of the Yearn vaults, a financial instrument that accrues value and has no payouts. The main complication is that the value accrual happens at a highly variable rate. We want to present the realized IRR of the vault over various periods of time.

A HackMD post explains the principles of calculating ROI for Yearn’s vaults. Alas, it contains some errors, which have propagated into the current implementations, resulting in incorrect estimated vault ROIs. The author argues against compounding due to an apparent misunderstanding of how it works, and instead suggests a linear extrapolation approach based on these four rules:

• Try to use data from two different points in time
• Assume growth is linear (because simply there is no other information we have)
• Construct a line using both points which we then extrapolate
• Calculate price at future data to display ROI.

The major flaw here is the incorrect assumption of linearity. Note that it is not merely a misleading or non-optimal way of evaluating performance; it constitutes a factual error. If you are mathematically astute, this may seem obvious, but since the issue has escaped detection for months, it is best to explain it here in detail.

We can use reductio ad absurdum to demonstrate that the value accrual of a vault cannot, in fact, be extrapolated using a linear function. For simplicity, assume that a vault, starting at a price per token of 1.0 exactly a month ago, is now at exactly 1.06, generating a ROI of 6%, and that growth has been produced evenly throughout the month. We’ll also ignore any fees. Alice and Bob both invested $10,000 in the vault at inception. Alice kept her funds there until withdrawing her entire balance of $10,600 today.

Bob, however, withdrew from the vault after the first day. Since growth is linear, as per our assumption, we know that 6% over a month is equivalent to 0.2% per day, and thus he received $10,020. He then returned it immediately into the vault. The next day, he repeated the same exercise, taking out his accrued $10,040.04 and immediately depositing it back. It was the same story the next day with $10,060.12 being moved.

You can already see where this is going. At the end of the month, Bob was able to withdraw $10,610, making ten bucks more than Alice from the exact same investment. To avoid any confusion about the time between withdrawals and deposits, we could assume Bob used a smart contract to make his daily withdrawal and re-deposit within a single transaction, so that his exit and entry prices were always equal.

It should be evident that Bob’s actions could not possibly have generated extra returns, and hence the extra $10 cannot exist. Therefore one of our assumptions must be incorrect.

The Fix

Just as the perimeter of a circle up close looks exactly like a straight line¹, the curve of an exponential function can appear indistinguishable from a linear one up close. It may seem like a 6% return spread over 30 days should equal a daily return of

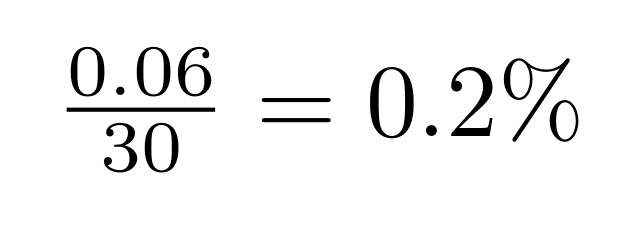
when in fact it is

which might look like something derived from compound interest, even though the vaults have no interest payments to compound. That is misleading, however: the same principle actually works in a number of vastly different domains (where the underlying values are said to have the same central tendency), including the intervals between musical notes.

Implementing this change in code requires changing just a few lines.

Conclusion

As the magnitude of the error is small, it is unlikely anyone has suffered harm from it, for example by making a poor allocation choice.

However, the mere existence of such a mistake can be instructive. Is it not somewhat arrogant of the author of the HackMD post to imagine that a vault (which isn’t that different from a mutual fund in mathematical terms) is an invention so unique that no existing formula can work on it? And given that many people have read the erroneous instructions and not spotted the problem, it serves as a reminder, if one were needed, that even the smartest people in the room are fallible.

---

1. More formally: the curvature of a circle approaches zero as its size increases. ↩︎

• defi
• basics